GridFilter¶
Description¶
Contais methods for working with cross-sections of the predetermined function. Function is represented as a matrix with values computed with the given grid.
The following operations can be done:
Get cross-section \(z=value\) with the given function value;
Get extended cross-section with the given function value and deviation from the original cross-section contour. Extended cross-section contains \(|z-value| <= deviation\) points;
Get extended cross-section with the given function value where deviation is computed automaticly and depends on the gradient vector length at cross-section points.
Constructors¶
GridFilter(const Eigen::MatrixXd & mat, double xStep, double yStep, int initDeviation, double gradInfl, double allowErr)
GridFilter(int rows, int columns, double* mat, double xStep, double yStep, int initDeviation, double gradInfl, double allowErr)
where
\(mat\) is matrix contains float values;
\(rows\) and \(columns\) are sizes of matrix \(mat\);
\(xStep\) and \(yStep\) are grid steps;
\(initDeviation\) is a multiplier for deviation, default is 1;
\(gradInfl\) is a multiplier for gradient component of deviation, default is 1;
\(allowErr\) is a tolerance for the original cross-section. Means that cross-section getter retuns result for \(z=value±allowErr\).
Member functions¶
Public:¶
GetCrossSectionOriginal(Eigen::MatrixXd & CSOmatTarget, double value, bool isCScomputed) writes a cross-section \(z=value±allowErr\) matrix without deviation to the CSOmatTarget matrix. Parameter isCScomputed helps to avoid compiting the same matrix twice.
GetCrossSectionExtended(Eigen::MatrixXd & CSEmatTarget, double value, int deviation, bool isCScomputed) writes a cross-section \(z=value±allowErr\) matrix with the given deviation to the CSEmatTarget matrix. Parameter isCScomputed helps to avoid compiting the same matrix twice.
GetCrossSectionExtendedAutoDev(Eigen::MatrixXd& CSEADmatTarget, double value) writes a cross-section \(z=value±allowErr\) matrix with the deviation computed automaticly by ComputeCurrentDeviation() function to the CSEADmatTarget matrix.
GetCrossSectionExtendedIrregular(Eigen::MatrixXd& CSEImatTarget, double value) writes a cross-section \(z=value±allowErr\) matrix with the different deviations at every point computed automaticly to the CSEImatTarget matrix.
GetInterestingPoints(Eigen::MatrixXd & IPTarget) writes an array of interesting points to the IPTarget matrix.
GetModifiedCrossSection(Eigen::MatrixXd & CSMTarget) is just getter for exteded cross-section (with auto deviation or not) without recomputation.
Protected:¶
ComputeGradient(double xStep, double yStep) computes gradients at every point for function values matrix with the given grid step:
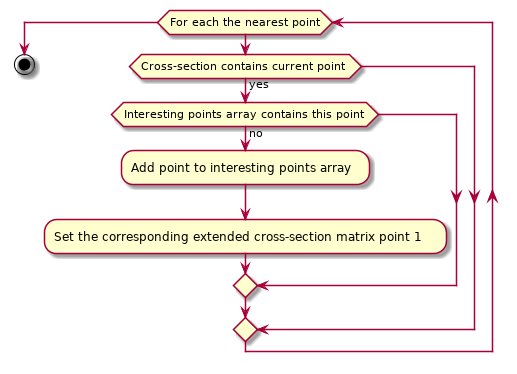
addPoints(int deviation) finds points of extended cross-section with the given deviation.
ComputeCrossSectionOriginal(double value) computes cross-section \(z = value ± allowErr\)
int ComputeCurrentDeviation()
Algorithm:
Compute non-zero elements in original cross-section;
For each element in matrixes compute respectivetly: \(dx[i, j] * CrossSectionOriginal[i, j]\) and \(dy[i, j] * CrossSectionOriginal[i, j]\) (this will leave only contour’s gradient points);
Find the sqrt of sum of squares (to fing the length of gradient vector);
Sum all this values;
Divide it by the number of non-zero values to find the avarage value of contour’s gradient;
Multiply it with the gradient multiplier (can be set at constructor, default is 1);
Product with multiplier InitialDeviation (can be set at constructor, default is 1).
Returns the value of deviation.
ComputeAbsGradMatrix() computes matrix contains gradient vector length at every point.
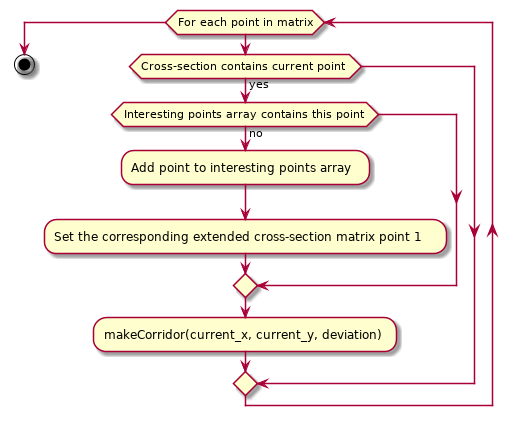
makeCorridor(int curr_x, int curr_y, int deviation) is auxiliary function for addPoints(int deviation). It fills the nearest points to the current points in extended cross-section matrix. As inputs there are coordinates of current point: \(curr\_x\) and \(curr\_y\) and deviation value that means that the square with side \(2 \times\text{deviation} + 1\) will be considered.