Introduction

The data flow paradigm has established itself as a powerful approach to machine learning. In fact, it is also very powerful for computational physics, although it is not used as much in the field. One of the complications is that physical models are much less homogeneous compared to ML, which makes their description a complicated task.

The GNA framework is designed to build mathematical models as lazy evaluated directed acyclic graphs. The syntax analyzer or parser introduces a way for a concise description and configuration of the models using math-like syntax, providing scalability and branching. The goal of the project is to develop a technique and a software to facilitate a generic analysis and input data description compatible with multiple backends, e.g. GNA.

The main goal of this project is to provide a set of tools for converting the textual representation of mathematical formulas into a directed graph. The textual representation of formulas corresponds to a certain DSL, which is specified by sets of tokens and rules in the form of a grammar.

General features

The module provides the following classes with certain aims: * GParser: parse input text into syntax tree (GTree); the class inherited from Lark.Tree * GPatternMatcher: do pattern matching procedure on syntax tree (GTree`) * GGraphBuilder: build graph (GAGraph) from syntax tree (GTree) or processed data (GData) from syntax tree * GDataBuilder: build data object (GData) from syntax tree (GTree) * GAGraph: graph class (inherited from pygraphviz.AGraph) * GData: data object of syntax tree leaf * GTree: syntax tree class (inherited from Lark.Tree) * GToken: grammar token class (inherited from Lark.Token`)

For the convenience of use, the GParser class includes GPatternMatcher, GGraphBuilder and GDataBuilder, so it is possible to use all the features by using only one method, namely GParser.parse.

The pattern matching procedure consists in setting a library of patterns (names, expressions and, if necessary, labels), using which the parser will replace the expressions encountered with the corresponding patterns.

Project structure and logic

The main parser class GParser inherits from the lark.Lark class. It uses LALR(1)-algorithm and contextual-lexer, which provide strict and fast parsing. Also cache provides 2-3 times faster parsing. The entry point for the parser is a sequence. See the Grammar chapter for more details.

Note

Each project class begins with a capital G to distinguish the inherited classes from the base classes of the **Lark-parser** and **PyGraphviz** packages, and to maintain a common style.

After the parsing method GParse.parse, any expression satisfying the grammar, in accordance with the rules and terminals specified in the file grammar.lark, is converted into a syntax tree implemented by the GTree class inherited from lark.tree.Tree, the nodes of which always end with the GToken class inherited from the lark.lexer.Token class. After that, the resulting tree is corrected: temporary nodes are removed and the structure of some nodes is replaced. If the argument make_identifiers=True is passed, GTree.identifier will be setted (for all the nodes). If the argument reset_counts=True is passed, *GTree._counts* will be resetted (the next parsed tree identifiers creation will start from zeros, else will continue previous counts).

Within the framework of the project, GPatternMatcher has been implemented, which allows replacing expressions after parsing with expressions from the specified library. You can perform a Pattern Matching directly in the GParse.parse method with the argument (pattern_matching=True) or manually: using the GParse.pattern_matching method or by instantiating a new GPatternMatcher class and using the GPatternMatcher.match method.

Finally, the project also implements GGraphBuilder, which implements the functionality of collecting the GAGraph graph from an existing GTree object. This procedure can also be performed within the GTree.parse method, passing the argument build_graph=True, or manually: using the GParse.build_graph method or by instantiating a new GGraphBuilder class and using the GGraphBuilder.build method.

Note

Each Builder class contains a main build method.

To construct the graph GAGraph, the GData class is used, which stores all the information about a specific node. To build the GData class (usually the GData list) from the GTree syntax tree (or the GTree list), the GDataBuilder class is designed.

For information on the structure of GData and GAGraph classes, see the chapter GAGraph and GData.

Grammar

Now the parser grammar implements next features:

• Parses any sequence, where sequence is:

  • variable (must be >= 4 symbols; the first letter is uppercase): var_1

  • transformation (must be >= 4 symbols; the first letter is lowercase) with/without arguments: Transf, Transf(arg), Transf | arg, where arg can be empty, variable, transformation, operation or several arguments, splitted by comma – Transf(arg1, arg2), Transf | arg1, arg2; the | argument rule means the next: Transf_1 | Transf_2 + Transf_3 | var_1, var_2 + var_3 the same as Transf_1(Transf_2 +Transf_3 (var_1, var_2 + var_3)); or other schematic example: a | b | c  + d*e the same as a(b(c+d*e));

  • special objects:

  • unityobject, one, unity, 1;

  • zeroobject, zero, null, 0. > Special objects are case insensitive, so you can use One, UNITY, UnityObject for the unity and Zero, NULL, ZeroObject for the zero.

  • operaion with/without arguments:

  • sum: var_1 + var_2, Energy + Spec, (Energy + Spec) | vars, …

  • subtraction: var_1 - var_2, Energy - Spec, (Energy - Spec) | vars, …

  • product: var_1 * var_2, Energy * Spec, (Energy * Spec) | vars, …

  • division: var_1 / var_2, Energy / Spec, (Energy / Spec) | vars, …

  • matrix product: Energy @ Spec, (Energy @ Spec) | vars, …

  • variable, transformation or operation with one index or multiple indexes, spiltted by comma: vars[i, j], Energy [dx, dy, dz], (Energy / Spec)[i, dx], …

  • transformation or operation with one reduction index or multiple reduction indexes, spiltted by comma: Energy {dx, dy, dz}, (Energy / Spec){i, dx}, …

    Note

    The standard grammar does not allow reduction with variable!

    Note

    The standard grammar does not allow index with reduction to the same object together!

    Note

    The standard grammar allows reduction without implicit index, but the graph building does not allow! See GAGraph and GData.

• assignment: newvar = vars[i], Power = Work/time, …

• newcall, which creates (on the graph building stage; see :ref:GAGraph and GData) a new instance of the transformation: Matrix * $Matrix, …

• comment, which is skipped: ... # this is comment.

• label to variable, transformation or operation: variable ::This is variable label::, Energy ::energy of the system::, (Work/time) ::the power::, …

• namespace, i.e. nested names: ns1.Energy, ns1.namespace2.ns123.variable, …

• Parses complicated sequences with mixed operations, brackets (), arguments, indexes, labels, comments, namespaces, etc.

Note

Spaces and tabs are ignored when parsing (in the standard grammar).

GTree features

The GTree class provides next features:

• Saving to the file by the GTree.save method;

• Contains identifier and label fields;

• The GTree.replace method, which replaces subtree by other tree and reurns the replaced tree;

• The GTree.get_similar_trees method, which returns a list with all trees that have a different look, but equal to the original;

• The GTree.remove_tokens method, which removes all the GTokens from the tree and returns the corrected tree;

• The GTree.removes_nodes_by method, which removes all the nodes by the data and returns the corrected tree;

• The GTree.get_by_identificator method, which finds the subtree by the identifier and returns it;

• The GTree.get_by_label method, which finds the subtree by the label and returns it.

GAGraph and GData

The GAGraph object is building from the GData list. The GData class is like a python dict, but with fixed structure:

• name (str);

• type (str);

• namespace (str);

• label (str);

• instance (int);

• arguments (list);

• indices (dict):

  • explicit (list);

  • implicit (list);

  • reduction (list).

For example, the constructed GData list for the string Spec[q]|var_1[i]*Matrix[j] would be:

[{'name': 'Spec', 'sname': 'Spec_1', 'type': 'transformation', 'namespace': '', 'instance': 1, 'arguments': ['Product_0'], 'indices': {'implicit': ['i', 'j'], 'explicit': ['q'], 'reduction': []}, 'label': {'default': 'Spec_1'}}, {'name': 'Product', 'sname': 'Product_0', 'type': 'transformation', 'namespace': '', 'instance': 0, 'arguments': ['var_1_1', 'Matrix_1'], 'indices': {'implicit': ['i', 'j'], 'explicit': [], 'reduction': []}, 'label': {'default': 'Product_0'}}, {'name': 'var_1', 'sname': 'var_1_1', 'type': 'variable', 'namespace': '', 'instance': 1, 'arguments': [], 'indices': {'implicit': [], 'explicit': ['i'], 'reduction': []}, 'label': {'default': 'var_1_1'}}, {'name': 'Matrix', 'sname': 'Matrix_1', 'type': 'transformation', 'namespace': '', 'instance': 1, 'arguments': [], 'indices': {'implicit': [], 'explicit': ['j'], 'reduction': []}, 'label': {'default': 'Matrix_1'}}]

The constructed GAGraph:

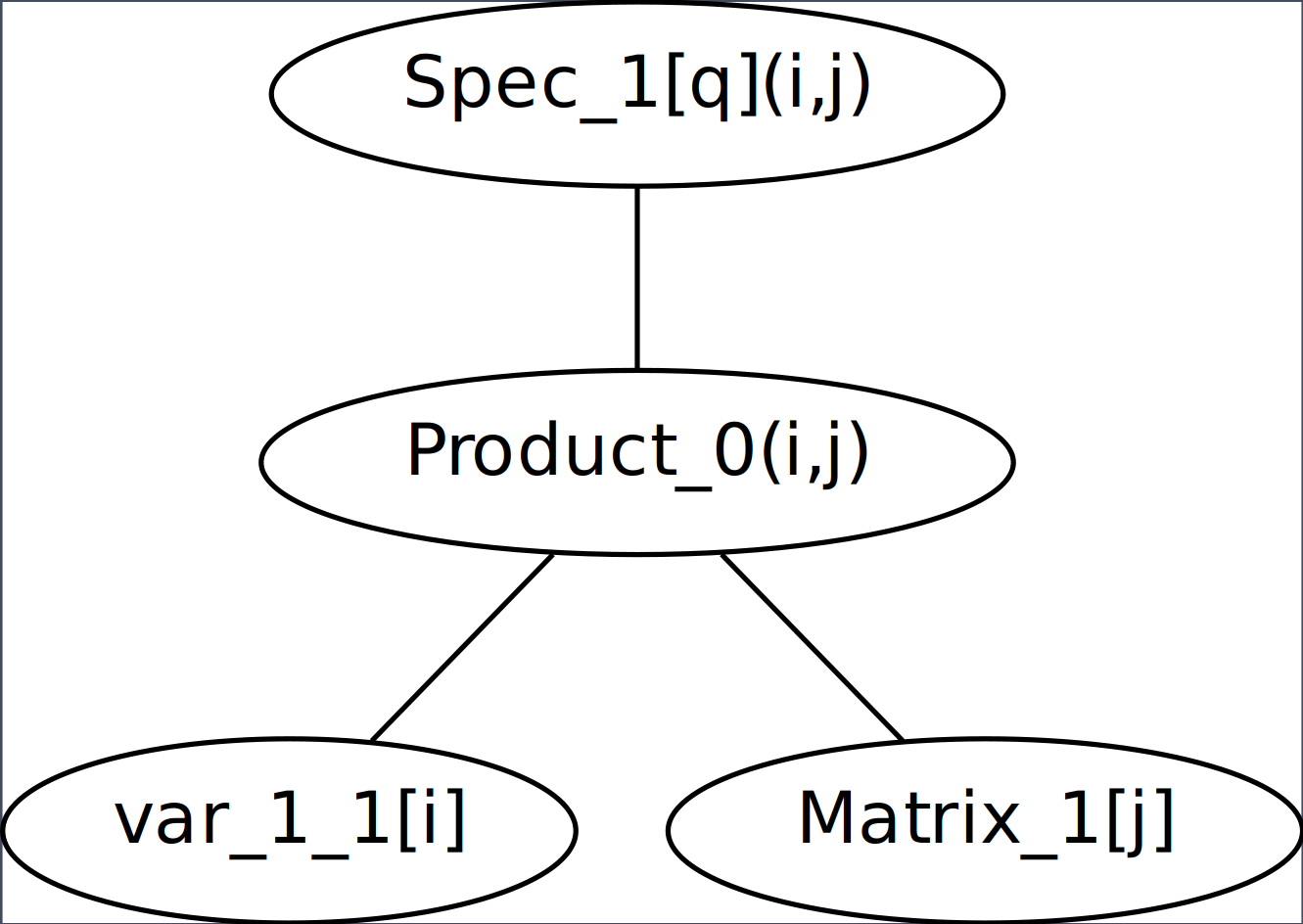
Textual representation of the GAGraph :class: toggle

strict graph “” {

graph [bb=”0,0,253.64,180”,

rankdir=BT

]; node [label=”N”]; Spec_1 [arguments=”[‘Product_0’]”,

height=0.5, indices=”{‘implicit’: [‘i’, ‘j’], ‘explicit’: [‘q’], ‘reduction’: []}”, instance=1, label=”Spec_1[q](i,j)”, labels=”{‘default’: ‘Spec_1’}”, name=Spec, pos=”123.9,162”, sname=Spec_1, type=transformation, uname=Spec_1, width=1.9859];

Product_0 [arguments=”[‘var_1_1’, ‘Matrix_1’]”,

height=0.5, indices=”{‘implicit’: [‘i’, ‘j’], ‘explicit’: [], ‘reduction’: []}”, instance=0, label=”Product_0(i,j)”, labels=”{‘default’: ‘Product_0’}”, name=Product, pos=”123.9,90”, sname=Product_0, type=transformation, uname=Product_0, width=2.0401];

Product_0 – Spec_1 [pos=”123.9,108.3 123.9,119.15 123.9,133.08 123.9,143.9”]; var_1_1 [arguments=”[]”,

height=0.5, indices=”{‘implicit’: [], ‘explicit’: [‘i’], ‘reduction’: []}”, instance=1, label=”var_1_1[i]”, labels=”{‘default’: ‘var_1_1’}”, name=var_1, pos=”55.895,18”, sname=var_1_1, type=variable, uname=var_1_1, width=1.5526];

var_1_1 – Product_0 [pos=”72.01,35.589 82.693,46.586 96.668,60.973 107.42,72.044”]; Matrix_1 [arguments=”[]”,

height=0.5, indices=”{‘implicit’: [], ‘explicit’: [‘j’], ‘reduction’: []}”, instance=1, label=”Matrix_1[j]”, labels=”{‘default’: ‘Matrix_1’}”, name=Matrix, pos=”191.9,18”, sname=Matrix_1, type=transformation, uname=Matrix_1, width=1.7151];

Matrix_1 – Product_0 [pos=”175.78,35.589 165.1,46.586 151.12,60.973 140.37,72.044”];

}

Note

The reduction index(es) must be in implicit index(es)!

Note

If newcall is parsed ($), on the GData building stage GDataBuilder will be trying to create a new instance for the transformation. If there are several instances of the transformation without newcall, the GDataBuilder will assign the same instance to all the instances of this transformation!

Installation

After cloning the repository, add the directory to PYTHONPATH:

git clone git@git.jinr.ru:gna/gparser.git
cd gparser
path=$(pwd)
export PYTHONPATH="$PYTHONPATH:$path"

The parser can now be used by importing the class:

>>> from gparser import GParser

Done!

Example

The next example shows how to use the GParser:

from gparser import GParser

parser = GParser(lib="tests/lib.yaml")
parse  = parser.parse

data = """
### ASSIGNMENTS ->
vars = something[a,b,c]
Days_in_second = ns1.ns2.Energy[i,l] | (vars + vars + something[a,b,c])
### ASSIGNMENTS <-

(Spec{k,l,i} | Matrix{m} | efflivetime[k]*alphan_rate[l, m] + Back{k,j}
                            | alphan_rate_norm[k,j] * Days_in_second{c})
+ (ABCD/vars[a,b,c] - Transf@Transf)*asda
"""

tree = parse(data, pattern_matching=True)
tree.print()
print()

out = parser.build_graph(newtree)

out.layout(prog='dot')
out.draw('graph.dot')

The saved graph graph.dot:

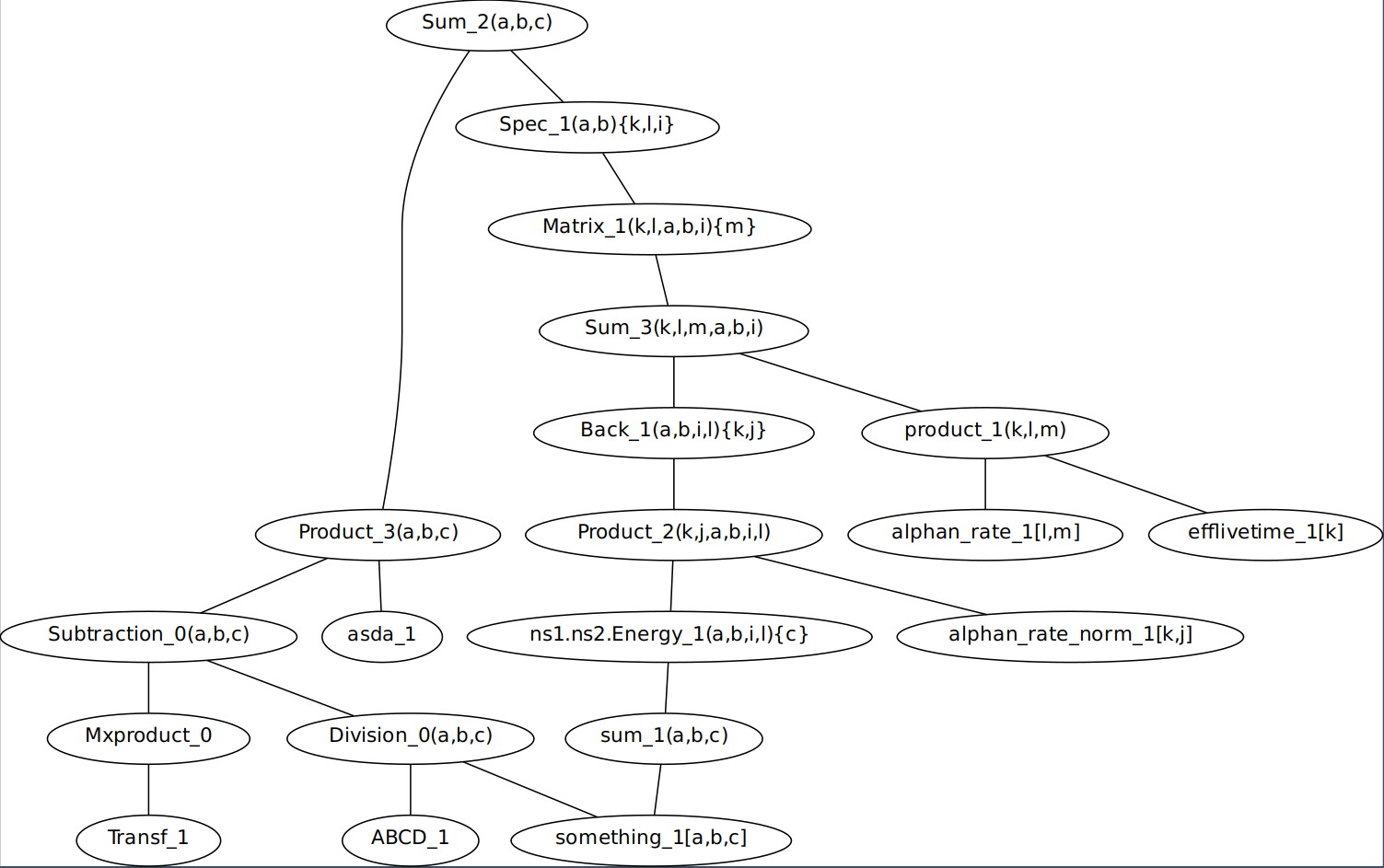
The console output

sequence

assignment

variable vars variable

something index

a b c

assignment

transformation Days_in_second transformation

namespace

ns1. ns2.

Energy index

i l

arg

sum_v

variable vars variable vars variable

something index

a b c

sum_t

reduction

transformation Spec index

k l i

arg

reduction

transformation Matrix index m arg

sum_t

product_v

variable

efflivetime index k

variable

alphan_rate index

l m

reduction

transformation Back index

k j

arg

product_t

variable

alphan_rate_norm index

k j

reduction

transformation Days_in_second index c

product_t

subtraction_t

division_t

transformation ABCD variable

vars index

a b c

mxproduct_t

transformation Transf transformation Transf

variable asda

strict graph “” {

graph [bb=”0,0,950.79,612”,

rankdir=BT

]; node [label=”N”]; something_1 [arguments=”[]”,

height=0.5, indices=”{‘implicit’: [], ‘explicit’: [‘a’, ‘b’, ‘c’], ‘reduction’: []}”, instance=1, label=”something_1[a,b,c]”, labels=”{‘default’: ‘something_1’}”, name=something, pos=”352.54,18”, sname=something_1, type=variable, uname=something_1, width=2.7442];

sum_1 [arguments=”[‘something_1’, ‘something_1’, ‘something_1’]”,

height=0.5, indices=”{‘implicit’: [‘a’, ‘b’, ‘c’], ‘explicit’: [], ‘reduction’: []}”, instance=1, label=”sum_1(a,b,c)”, labels=”{‘default’: ‘sum_1’}”, name=sum, pos=”259.54,90”, sname=sum_1, type=variable, uname=sum_1, width=1.9318];

something_1 – sum_1 [pos=”330.5,35.589 315.57,46.828 295.93,61.609 281.1,72.772”]; Division_0 [arguments=”[‘ABCD_1’, ‘something_1’]”,

height=0.5, indices=”{‘implicit’: [‘a’, ‘b’, ‘c’], ‘explicit’: [], ‘reduction’: []}”, instance=0, label=”Division_0(a,b,c)”, labels=”{‘default’: ‘Division_0’}”, name=Division, pos=”522.54,90”, sname=Division_0, type=transformation, uname=Division_0, width=2.4192];

something_1 – Division_0 [pos=”390.69,34.709 418.99,46.359 457.35,62.154 485.4,73.704”]; Energy_1 [arguments=”[‘sum_1’]”,

height=0.5, indices=”{‘implicit’: [‘a’, ‘b’, ‘i’, ‘l’], ‘explicit’: [], ‘reduction’: [‘c’]}”, instance=1, label=”ns1.ns2.Energy_1(a,b,i,l){c}”, labels=”{‘default’: ‘ns1.ns2.Energy_1’}”, name=Energy, namespace=”ns1.ns2”, pos=”215.54,162”, sname=Energy_1, type=transformation, uname=Energy_1, width=3.9719];

sum_1 – Energy_1 [pos=”248.89,107.95 242.08,118.79 233.26,132.82 226.4,143.72”]; Subtraction_0 [arguments=”[‘Division_0’, ‘Mxproduct_0’]”,

height=0.5, indices=”{‘implicit’: [‘a’, ‘b’, ‘c’], ‘explicit’: [], ‘reduction’: []}”, instance=0, label=”Subtraction_0(a,b,c)”, labels=”{‘default’: ‘Subtraction_0’}”, name=Subtraction, pos=”743.54,162”, sname=Subtraction_0, type=transformation, uname=Subtraction_0, width=2.9067];

Division_0 – Subtraction_0 [pos=”568.07,105.42 605.34,117.23 657.92,133.88 695.79,145.87”]; Product_2 [arguments=”[‘alphan_rate_norm_1’, ‘Energy_1’]”,

height=0.5, indices=”{‘implicit’: [‘k’, ‘j’, ‘a’, ‘b’, ‘i’, ‘l’], ‘explicit’: [], ‘reduction’: []}”, instance=2, label=”Product_2(k,j,a,b,i,l)”, labels=”{‘default’: ‘Product_2’}”, name=Product, pos=”498.54,234”, sname=Product_2, type=transformation, uname=Product_2, width=2.9067];

Energy_1 – Product_2 [pos=”277.3,178.28 326.09,190.34 393.66,207.06 441.25,218.83”]; Product_3 [arguments=”[‘Subtraction_0’, ‘asda_1’]”,

height=0.5, indices=”{‘implicit’: [‘a’, ‘b’, ‘c’], ‘explicit’: [], ‘reduction’: []}”, instance=3, label=”Product_3(a,b,c)”, labels=”{‘default’: ‘Product_3’}”, name=Product, pos=”743.54,234”, sname=Product_3, type=transformation, uname=Product_3, width=2.4012];

Subtraction_0 – Product_3 [pos=”743.54,180.3 743.54,191.15 743.54,205.08 743.54,215.9”]; Back_1 [arguments=”[‘Product_2’]”,

height=0.5, indices=”{‘implicit’: [‘a’, ‘b’, ‘i’, ‘l’], ‘explicit’: [], ‘reduction’: [‘k’, ‘j’]}”, instance=1, label=”Back_1(a,b,i,l){k,j}”, labels=”{‘default’: ‘Back_1’}”, name=Back, pos=”498.54,306”, sname=Back_1, type=transformation, uname=Back_1, width=2.7442];

Product_2 – Back_1 [pos=”498.54,252.3 498.54,263.15 498.54,277.08 498.54,287.9”]; Sum_3 [arguments=”[‘product_1’, ‘Back_1’]”,

height=0.5, indices=”{‘implicit’: [‘k’, ‘l’, ‘m’, ‘a’, ‘b’, ‘i’], ‘explicit’: [], ‘reduction’: []}”, instance=3, label=”Sum_3(k,l,m,a,b,i)”, labels=”{‘default’: ‘Sum_3’}”, name=Sum, pos=”498.54,378”, sname=Sum_3, type=transformation, uname=Sum_3, width=2.6359];

Back_1 – Sum_3 [pos=”498.54,324.3 498.54,335.15 498.54,349.08 498.54,359.9”]; Sum_2 [arguments=”[‘Spec_1’, ‘Product_3’]”,

height=0.5, indices=”{‘implicit’: [‘a’, ‘b’, ‘c’], ‘explicit’: [], ‘reduction’: []}”, instance=2, label=”Sum_2(a,b,c)”, labels=”{‘default’: ‘Sum_2’}”, name=Sum, pos=”646.54,594”, sname=Sum_2, type=transformation, uname=Sum_2, width=1.9679];

Spec_1 [arguments=”[‘Matrix_1’]”,

height=0.5, indices=”{‘implicit’: [‘a’, ‘b’], ‘explicit’: [], ‘reduction’: [‘k’, ‘l’, ‘i’]}”, instance=1, label=”Spec_1(a,b){k,l,i}”, labels=”{‘default’: ‘Spec_1’}”, name=Spec, pos=”586.54,522”, sname=Spec_1, type=transformation, uname=Spec_1, width=2.5817];

Spec_1 – Sum_2 [pos=”601.07,539.95 610.5,550.95 622.75,565.24 632.15,576.21”]; Matrix_1 [arguments=”[‘Sum_3’]”,

height=0.5, indices=”{‘implicit’: [‘k’, ‘l’, ‘a’, ‘b’, ‘i’], ‘explicit’: [], ‘reduction’: [‘m’]}”, instance=1, label=”Matrix_1(k,l,a,b,i){m}”, labels=”{‘default’: ‘Matrix_1’}”, name=Matrix, pos=”549.54,450”, sname=Matrix_1, type=transformation, uname=Matrix_1, width=3.1594];

Matrix_1 – Spec_1 [pos=”558.5,467.95 564.23,478.79 571.65,492.82 577.41,503.72”]; Sum_3 – Matrix_1 [pos=”510.89,395.95 518.79,406.79 529.01,420.82 536.96,431.72”]; product_1 [arguments=”[‘efflivetime_1’, ‘alphan_rate_1’]”,

height=0.5, indices=”{‘implicit’: [‘k’, ‘l’, ‘m’], ‘explicit’: [], ‘reduction’: []}”, instance=1, label=”product_1(k,l,m)”, labels=”{‘default’: ‘product_1’}”, name=product, pos=”279.54,306”, sname=product_1, type=variable, uname=product_1, width=2.4192];

product_1 – Sum_3 [pos=”324.65,321.42 361.97,333.35 414.75,350.22 452.36,362.24”]; efflivetime_1 [arguments=”[]”,

height=0.5, indices=”{‘implicit’: [], ‘explicit’: [‘k’], ‘reduction’: []}”, instance=1, label=”efflivetime_1[k]”, labels=”{‘default’: ‘efflivetime_1’}”, name=efflivetime, pos=”82.543,234”, sname=efflivetime_1, type=variable, uname=efflivetime_1, width=2.2929];

efflivetime_1 – product_1 [pos=”123.84,249.67 157.24,261.54 204.06,278.18 237.62,290.1”]; alphan_rate_1 [arguments=”[]”,

height=0.5, indices=”{‘implicit’: [], ‘explicit’: [‘l’, ‘m’], ‘reduction’: []}”, instance=1, label=”alphan_rate_1[l,m]”, labels=”{‘default’: ‘alphan_rate_1’}”, name=alphan_rate, pos=”279.54,234”, sname=alphan_rate_1, type=variable, uname=alphan_rate_1, width=2.69];

alphan_rate_1 – product_1 [pos=”279.54,252.3 279.54,263.15 279.54,277.08 279.54,287.9”]; alphan_rate_norm_1 [arguments=”[]”,

height=0.5, indices=”{‘implicit’: [], ‘explicit’: [‘k’, ‘j’], ‘reduction’: []}”, instance=1, label=”alphan_rate_norm_1[k,j]”, labels=”{‘default’: ‘alphan_rate_norm_1’}”, name=alphan_rate_norm, pos=”498.54,162”, sname=alphan_rate_norm_1, type=variable, uname=alphan_rate_norm_1, width=3.3941];

alphan_rate_norm_1 – Product_2 [pos=”498.54,180.3 498.54,191.15 498.54,205.08 498.54,215.9”]; Product_3 – Sum_2 [pos=”738.28,252.3 730.68,278.86 717.54,331.39 717.54,377 717.54,377 717.54,377 717.54,451 717.54,492.6 708.22,503.34 688.54,540 681.44,

553.24 670.94,566.49 662.21,576.43”];

ABCD_1 [arguments=”[]”,

height=0.5, indices=”{‘implicit’: [], ‘explicit’: [], ‘reduction’: []}”, instance=1, label=ABCD_1, labels=”{‘default’: ‘ABCD_1’}”, name=ABCD, pos=”522.54,18”, sname=ABCD_1, type=transformation, uname=ABCD_1, width=1.336];

ABCD_1 – Division_0 [pos=”522.54,36.303 522.54,47.154 522.54,61.083 522.54,71.896”]; Mxproduct_0 [arguments=”[‘Transf_1’, ‘Transf_1’]”,

height=0.5, indices=”{‘implicit’: [], ‘explicit’: [], ‘reduction’: []}”, instance=0, label=Mxproduct_0, labels=”{‘default’: ‘Mxproduct_0’}”, name=Mxproduct, pos=”743.54,90”, sname=Mxproduct_0, type=transformation, uname=Mxproduct_0, width=1.9859];

Mxproduct_0 – Subtraction_0 [pos=”743.54,108.3 743.54,119.15 743.54,133.08 743.54,143.9”]; Transf_1 [arguments=”[]”,

height=0.5, indices=”{‘implicit’: [], ‘explicit’: [], ‘reduction’: []}”, instance=1, label=Transf_1, labels=”{‘default’: ‘Transf_1’}”, name=Transf, pos=”743.54,18”, sname=Transf_1, type=transformation, uname=Transf_1, width=1.4082];

Transf_1 – Mxproduct_0 [pos=”743.54,36.303 743.54,47.154 743.54,61.083 743.54,71.896”]; asda_1 [arguments=”[]”,

height=0.5, indices=”{‘implicit’: [], ‘explicit’: [], ‘reduction’: []}”, instance=1, label=asda_1, labels=”{‘default’: ‘asda_1’}”, name=asda, pos=”908.54,162”, sname=asda_1, type=variable, uname=asda_1, width=1.1735];

asda_1 – Product_3 [pos=”879.8,175.19 852.01,186.98 809.8,204.89 779.73,217.65”];

}

previous

Welcome to The GNA Parser’s documentation!

next

Reference guide