7.1.3. WeightedSum transformation¶
After getting familiar with how variables are defined it is the time to start using them with transformations. The first
transformation we will consider is WeightedSum. WeightedSum transformation implements the following sum:
where \(A_i\) is an array bound to the transformation input \(i\), \(\omega_i\) is a weight bound to the transformation from the namespace. Let us look at the example:
1import load
2from gna.env import env
3import gna.constructors as C
4import numpy as np
5from matplotlib import pyplot as plt
6from gna.bindings import common
7
8# Make a variable for global namespace
9ns = env.globalns
10
11# Create a parameter in the global namespace
12w1 = ns.defparameter('a', central=1.0, free=True, label='weight 1')
13w2 = ns.defparameter('b', central=0.1, free=True, label='weight 2')
14w3 = ns.defparameter('c', central=0.05, free=True, label='weight 3')
15
16# Print the list of parameters
17ns.printparameters(labels=True)
18print()
19
20# Create x and several functions to be added with weights
21x = np.linspace(-1.0*np.pi, 1.0*np.pi, 500)
22a1 = C.Points(np.sin(x))
23a2 = C.Points(np.sin(16.0*x))
24a3 = C.Points(np.cos(16.0*x))
25outputs = [a.points.points for a in (a1, a2, a3)]
26
27# Initialize the WeightedSum with list of variables and list of outputs
28weights = ['a', 'b', 'c']
29wsum = C.WeightedSum(weights, outputs)
30wsum.print()
31
32# Do some plotting
33fig = plt.figure()
34ax = plt.subplot( 111 )
35ax.minorticks_on()
36ax.grid()
37ax.set_xlabel( 'x' )
38ax.set_ylabel( 'f(x)' )
39ax.set_title(r'$a\,\sin(x)+b\,\sin(16x)+c\,\cos(16x)$')
40
41label = 'a={}, b={}, c={}'.format(w1.value(), w2.value(), w3.value())
42wsum.sum.sum.plot_vs(x, label=label)
43
44w2.push(0.0)
45w3.push(0.0)
46label = 'a={}, b={}, c={}'.format(w1.value(), w2.value(), w3.value())
47wsum.sum.sum.plot_vs(x, label=label)
48
49w1.push(0.0)
50w2.pop()
51label = 'a={}, b={}, c={}'.format(w1.value(), w2.value(), w3.value())
52wsum.sum.sum.plot_vs(x, label=label)
53
54w2.push(0.0)
55w3.pop()
56label = 'a={}, b={}, c={}'.format(w1.value(), w2.value(), w3.value())
57wsum.sum.sum.plot_vs(x, label=label)
58
59ax.legend(loc='lower right')
60
61plt.show()
The example implements the following formula:
where \(a\), \(b\) and \(c\) are variables, initialized as follows:
w1 = ns.defparameter('a', central=1.0, free=True, label='weight 1')
w2 = ns.defparameter('b', central=0.1, free=True, label='weight 2')
w3 = ns.defparameter('c', central=0.05, free=True, label='weight 3')
The WeightedSum constructor is similar to the one for Sum with the only addition: a list of variables names
should be passed as the first argument:
weights = ['a', 'b', 'c']
wsum = C.WeightedSum(weights, outputs)
The second argument is either list of outputs or list of names to give to the inputs. In the latter case the inputs should be bounded to outputs of other transformations manually as it was done in tutorials for transformations Sum and Product.
The contents of the WeightedSum from the example above is the following:
[obj] WeightedSum: 1 transformation(s)
0 [trans] sum: 3 input(s), 1 output(s)
0 [in] a -> [out] points: array 1d, shape 500, size 500
1 [in] b -> [out] points: array 1d, shape 500, size 500
2 [in] c -> [out] points: array 1d, shape 500, size 500
0 [out] sum: array 1d, shape 500, size 500
Variables, relative to namespace "":
a = 1 │ 1± inf [free] │ weight 1
b = 0.1 │ 0.1± inf [free] │ weight 2
c = 0.05 │ 0.05± inf [free] │ weight 3
Note, that print() method now prints the variables on which GNAObject depends.
After initializing the object we make four plots:
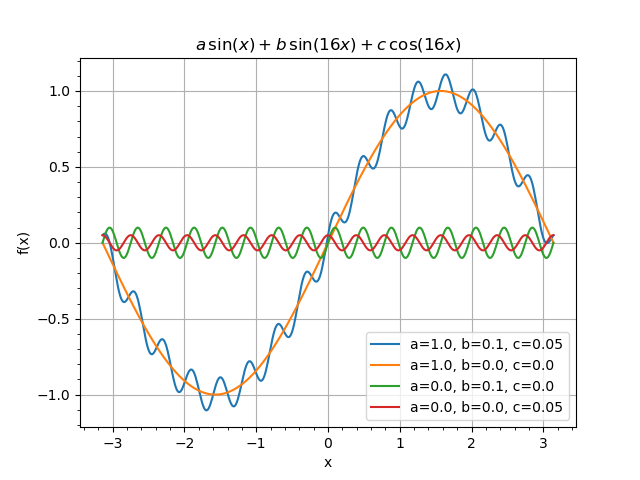
A set of WeightedSum plots for different values of the parameters.¶
First (blue) line corresponds to the initial parameters \(a=1.0\), \(b=0.1\) and \(c=0.05\). Then we switch of fast oscillating components with
w2.push(0.0)
w3.push(0.0)
Here we have used push(value) method, that sets the value of the parameter and saves the previous one. The previous value may then be retrieved by pop() method.
The second line (orange) corresponds to the main frequency. Then we disable main frequency and enable the first secondary frequency by:
w1.push(0.0)
w2.pop()
The green line corresponds to this. The last minor component (red) is plotted after changing the parameters:
w2.push(0.0)
w3.pop()
7.1.4. Working with nested namespaces¶
Now let us repeat the example above in a different setting.
1import load
2from gna.env import env
3import gna.constructors as C
4import numpy as np
5from matplotlib import pyplot as plt
6from gna.bindings import common
7
8# Make a variable for global namespace
9ns = env.globalns
10
11# Create a parameter in the global namespace
12ns.defparameter('a', central=1.0, free=True, label='weight 1 (global)')
13ns.defparameter('b', central=-0.1, free=True, label='weight 2 (global)')
14ns.defparameter('group.a', central=0.5, free=True, label='weight 1 (local)')
15ns.defparameter('group.b', central=0.00, free=True, label='weight 2 (local)')
16ns.defparameter('group.c', central=0.05, free=True, label='weight 3 (local)')
17
18# Print the list of parameters
19ns.printparameters(labels=True)
20print()
21
22# Create x and several functions to be added with weights
23x = np.linspace(-1.0*np.pi, 1.0*np.pi, 500)
24a1 = C.Points(np.sin(x))
25a2 = C.Points(np.sin(16.0*x))
26a3 = C.Points(np.cos(16.0*x))
27outputs = [a.points.points for a in (a1, a2, a3)]
28
29# Initialize the WeightedSum with list of variables and list of outputs
30weights1 = ['a', 'b', 'group.c']
31wsum1 = C.WeightedSum(weights1, outputs)
32
33weights2 = ['a', 'b', 'c']
34with ns('group'):
35 wsum2 = C.WeightedSum(weights2, outputs)
36
37wsum1.print(); print()
38wsum2.print(); print()
39
40# Do some plotting
41fig = plt.figure()
42ax = plt.subplot( 111 )
43ax.minorticks_on()
44ax.grid()
45ax.set_xlabel( 'x' )
46ax.set_ylabel( 'f(x)' )
47ax.set_title( r'$a\,\sin(x)+b\,\sin(16x)+c\,\cos(16x)$' )
48
49wsum1.sum.sum.plot_vs(x, label='Weighted sum 1: a={a}, b={b}, c={c}'.format(**wsum1.variablevalues()))
50wsum2.sum.sum.plot_vs(x, label='Weighted sum 2: a={a}, b={b}, c={c}'.format(**wsum2.variablevalues()))
51
52ax.legend(loc='lower right')
53
54plt.show()
We define two sets of variables. Parameters \(a\) and \(b\) in the global namespace and parameters \(a\), \(b\) and \(c\) in namespace group.
ns.defparameter('a', central=1.0, free=True, label='weight 1 (global)')
ns.defparameter('b', central=-0.1, free=True, label='weight 2 (global)')
ns.defparameter('group.a', central=0.5, free=True, label='weight 1 (local)')
ns.defparameter('group.b', central=0.00, free=True, label='weight 2 (local)')
ns.defparameter('group.c', central=0.05, free=True, label='weight 3 (local)')
Then we create two instances of WeightedSum with similar inputs, but depending on different variables. First:
weights1 = ['a', 'b', 'group.c']
wsum1 = C.WeightedSum(weights1, outputs)
depends on variables \(a\) and \(b\) from global namespace and variable \(c\) from namespace group. The dependence is reflected by the output:
Variables, relative to namespace "":
a = 1 │ 1± inf [free] │ weight 1 (global)
b = -0.1 │ -0.1± inf [free] │ weight 2 (global)
c = 0.05 │ 0.05± inf [free] │ weight 3 (local) [group.c]
Note the full path group.c printed for the variable \(c\).
The second WeightedSum is created in a nested namespace group:
weights2 = ['a', 'b', 'c']
with ns('group'):
wsum2 = C.WeightedSum(weights2, outputs)
Note that since the variables are now taken from the namespace group the local path c is used for variable \(c\). The switching to the group group is done via with ns(‘group’): statement. All the code within the scope of the with statement will work with variables from the namespace group.
The printout of the second WeightedSum now refers to the variables from the group:
Variables, relative to namespace "group":
a = 0.5 │ 0.5± inf [free] │ weight 1 (local)
b = 0 │ 0± inf [free] │ weight 2 (local)
c = 0.05 │ 0.05± inf [free] │ weight 3 (local)
Instances of WeightedSum depend on different sets of variables. We then plot them with
wsum1.sum.sum.plot_vs(x, label='Weighted sum 1: a={a}, b={b}, c={c}'.format(**wsum1.variablevalues()))
wsum2.sum.sum.plot_vs(x, label='Weighted sum 2: a={a}, b={b}, c={c}'.format(**wsum2.variablevalues()))
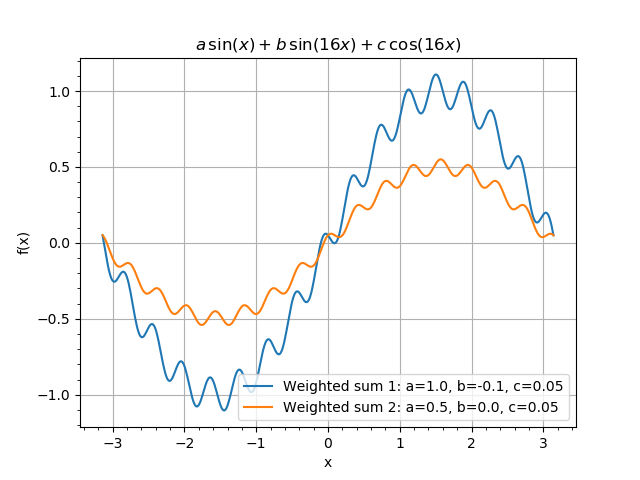
A set of WeightedSum plots for different values of the parameters.¶
To make the legend we have used variablevalues() method. It returns the dictionary with short variable names and
values and can be used within string formatting functions.
Note
variablevalues() and print() methods take care only on the variables the transformation depends directly. It
knows nothing about variables the input transformation depend on.