EnergyResolutionC

Description

Applies energy resolution to the histogram of events binned in \(E_{\text{vis}}\).

The transformation may be configured within detector_eres_common3 bundle.

Inputs

1. 'smear.Nvis' — one-dimensional histogram of number of events \(N_{\text{vis}}\).

Outputs

1. 'smear.Nrec' one-dimensional smeared histo of number of events \(N_{\text{rec}}\)

Variables

1. Eres_a — \(a\), 1. Eres_b — \(b\), 1. Eres_c — \(c\)

are the parameters of the energy resolution formula. See below.

Tests

Use the following commands for the usage example and testing:

./tests/detector/test_eres.py -s

Implementation

The smeared histo \(N_{\text{rec}}\) and true \(N_{\text{vis}}\) are connected through a matrix transformation:

\[N^{\text{rec}}_i = \sum_j V^{\text{res}}_{ij} N^{\text{vis}}_j,\]

where \(N^{\text{rec}}_i\) is a reconstructed number of events in a i-th bin, \(N^{\text{vis}}_j\) is a true number of events in a j-th bin and \(V^{\text{res}}_{ij}\) is a probability for events to flow from j-th to i bin.

That probability is given by:

\[V^{\text{res}}_{ij} = \frac{1}{\sqrt{2 \pi} \sigma(E_j)} \exp \left( - \frac{(E_j - E_i)^2}{2 \sigma^2(E_j)} \right),\]

where \(\sigma(E_j)\) is:

\[\sigma(E_j) = E_j \sqrt{ a^2 + \frac{b^2}{E_j} + \left( \frac{c}{E_j}\right)^2}\]

where \(a\), \(b\), \(c\) are resolution parameters.

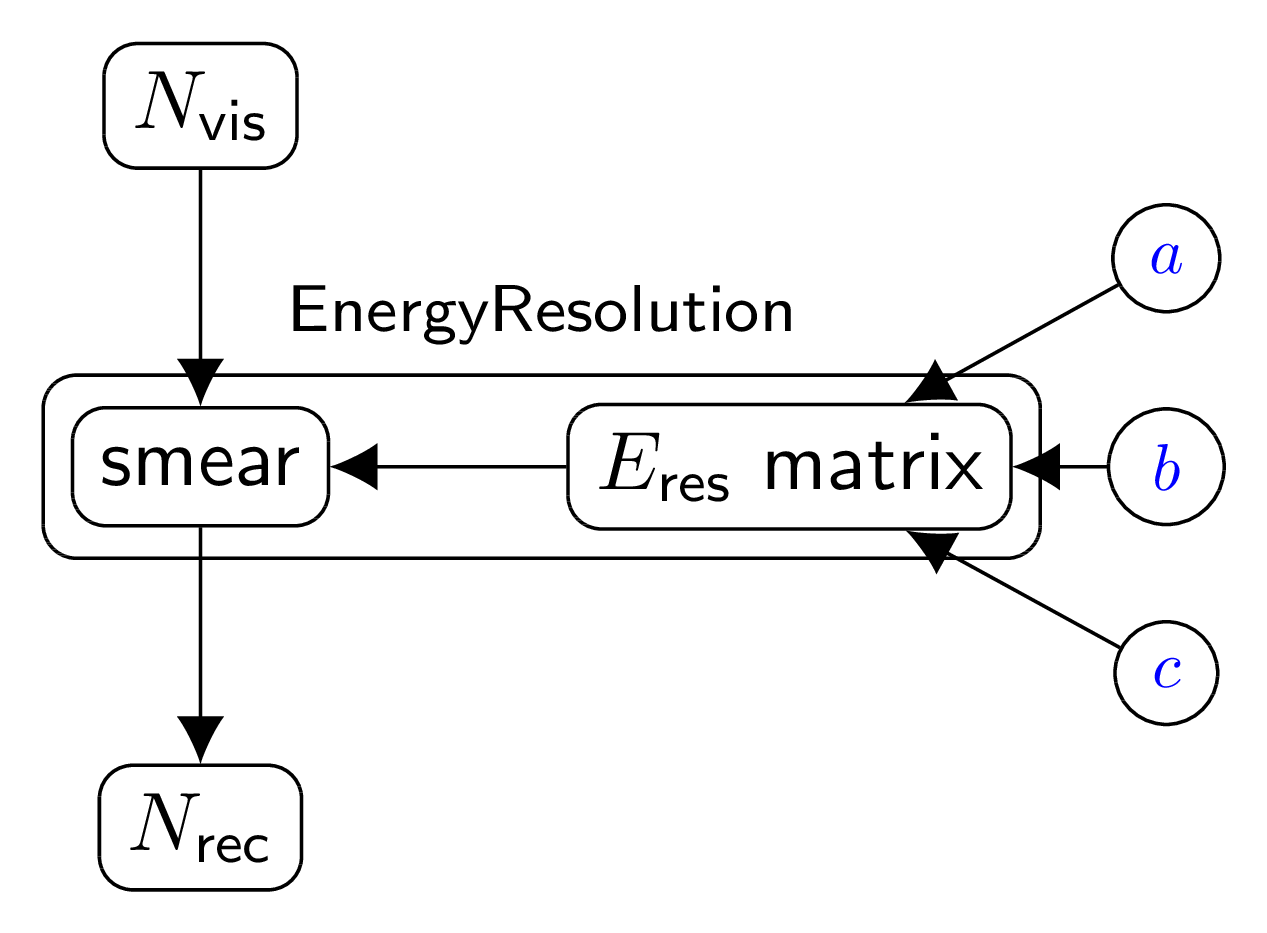
Energy resolution bundle scheme.