HistNonlinearity

Description

Simulates the effect of the x-axis scale distortion, usually non-linear. It is deterministic effect. May be used for example to simulate energy non-linearity effect.

HistNonlinearity contains two transformations:

1. Matrix transformation, that calculates ‘smearing’ matrix for given distortion.

2. Smear transformation, that actually applies the smearing matrix.

Note

Use HistNonlinearity for cases when Matrix form is desirable. In other cases consider using smooth integration scaling.

Inputs

The inputs of the Matrix and Smear transformations should be provided via set(bin_edges, bin_edges_modified, ntrue) method.

Arguments

1. bool propagate_matrix=false. While false, the smearing matrix will be used only within HistNonlinearity class instance, but will not be accessible via Matrix transformation output.

Constants

The class contains two constants range_min=-1e100 and range_max=+1e100, that may be set via set_range(min, max) method. All the bins with modified edges below range_min or above range_max are ignored.

Tests

Use the following commands for the usage example and testing:

./tests/detector/test_nonlinearity.py -s
./tests/detector/test_nonlinearity_matrix.py -s

Matrix transformation

Description

For a given bin edges distortion calculates the ‘smearing’ matrix. The matrix usually will have only a ‘distorted’ diagonal elements and thus is stored as a sparse matrix.

Inputs

1. 'matrix.Edges' — ­the original bin edges. These edges will be also used to project the result to.

2. 'matrix.EdgesModified' — the modified bin edges of the same size as 'matrix.Edges'.

Outputs

1. 'matrix.FakeMatrix' — the ‘smearing’ matrix. Will be written only if propagate_matrix is true.

Implementation

Assume on has a set of bin edges \(E_i\) and energy non-linearity function \(f(E)\). The distortion result is thus \(E_i' = f(E_i)\). The algorithm projects each distorted bin \((E_i', E_{i+1}')\) to the original grid \(E\). The relative fraction of bin \((E_i', E_{i+1}')\) that overlaps with original bin \(j\) then defines the matrix element \(C_{ji}\). The matrix \(C\) implements the conversion from the non-distorted spectrum \(S\) to distorted one:

\[S_j' = C_{ji} S_i.\]

The formula for \(C_{ji}\), which defines the transition from bin \(i\) to \(j\) may be written as follows:

\[C_{ji} = \frac{B-A}{f(E_{i+1}) - f(E_i)},\]

where the interval \((A,B)\) is defined as intersection:

\[(A,B) = (E_j, E_{j+1}) \cap (f(E_{i}),f(E_{i+1}) ).\]

Since each column \(C_{ji}\) represents the smearing of a single bin, the sum of a column is 1:

\[\sum\limits_j C_{ij} = 1,\]

except the near boundary cases, when part of the events flows out of the histogram.

The algorithm may be illustrated with the following figure.

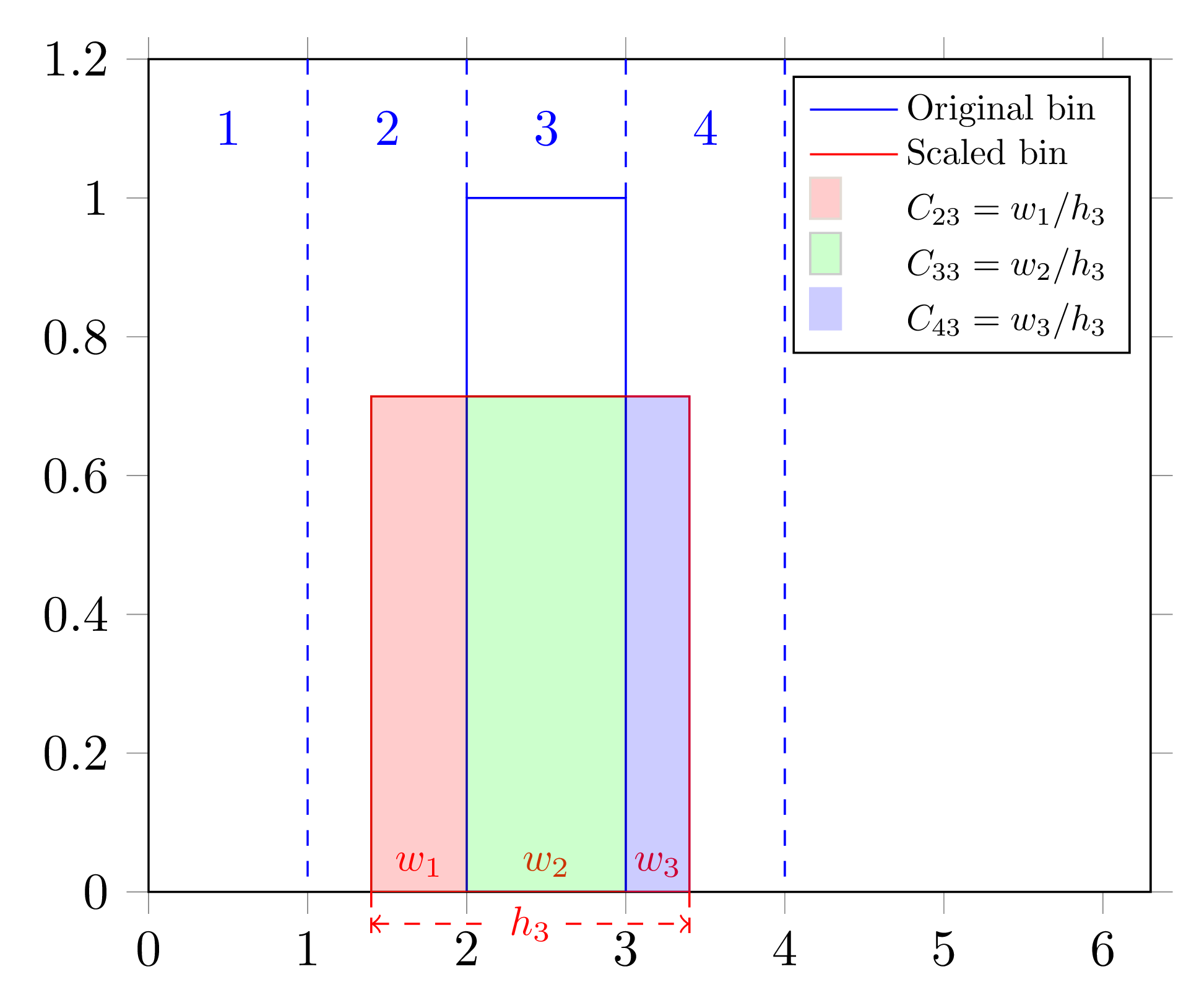
An illustration of HistNonlinearity applied to a single bin.

Here the original blue bin 3 with edges \((2,3)\) is distorted by non-linearity function to \((1.4,3.4)\). The resulting bin overlaps with bins 2, 3 and 4. The weights \(C_{23}\), \(C_{33}\) and \(C_{34}\) are widths of the overlaps \(w_1\), \(w_2\) and \(w_3\) divided by the full modified bin width \(h\):

\[C_{23} = \frac{w_1}{h},\quad\quad\quad\quad C_{33} = \frac{w_2}{h},\quad\quad\quad\quad C_{43} = \frac{w_3}{h}.\]

All the other weights are 0.

Note, that the distorted bin may be completely off the original bin, so that \(C_{ii}=0\).

The matrix is built using effective single passage algorithm, that sequentially iterates adjacent bin edges from \(E\) and \(f(E)\). The binary search is called only once to determine the entry point.

All the bins with modified edges below range_min or above range_max are ignored. See Constants.

Smear transformation

Description

Applies sparse ‘smearing’ matrix to the histogram of events binned in \(E_{\text{true}}\).

Inputs

1. 'smear.Ntrue' — one-dimensional histogram of number of events \(N_{\text{true}}\).

2. 'smear.FakeMatrix' — ‘smearing’ matrix. Not read, but used only for the taint-flag propagation.

Outputs

1. 'smear.Nrec' one-dimensional smeared histo of number of events \(N_{\text{vis}}\)